Hierarchical Cumulative Voting Prioritization

 

What is it?

Hierarchical Cumulative Voting (HCV) Prioritization is a variant of the ratio-scale Cumulative Voting (CV) prioritization technique. Cumulative Voting is normally done against ALL items of same level of abstraction at the same time (for example, the entire set of detailed requirements). This means the standard CV process does not scale well as you add more items to be prioritized. To address this issue, the Hierarchical Cumulative Voting (HCV) variant of CV was developed by Berander and Jonsson^[3] as an answer to some of the scalability issues when there are a larger number of items to be prioritized.

Similar to the Hierarchical MoSCoW technique, with HCV the items being prioritized are first broken into levels of abstraction, and then each item at the highest level of abstraction is further decomposed into greater levels of detail, with each level of greater detail being considered a separate level of abstraction.  These items could be features, functions, requirements levels, or similar breakdowns, but should feature high levels of cohesion with their lower-level children and low levels of cohesion with their siblings.  [See the Decomposition wiki entry for more discussion of coupling and cohesion.]

HCV uses the standard Cumulative Voting (CV) process, but instead of applying to all items of the same level of abstraction at once, each group is voted on separately at each level of abstraction. HCV then also applies a normalization process that will allow you to compare the priorities of items that are in different groups.

 

---

Why do it?

See the Prioritization wiki page for a discussion of why to prioritize.

However, the major advantages of Hierarchical Cumulative Voting is that it can be relatively easily to apply to even large items sets that need to be prioritized; and by breaking the items into discreet sets (of features, functions, etc.) at increasing levels of abstraction, stakeholders can focus their attention on limited numbers of items without being overwhelmed by having to analyze all items at a single level of abstraction at once. HCV allows stakeholders to provide a high-level of nuanced prioritization information.

 

---

How do I do it?

This assumes you have evaluated your prioritization needs and decided that Hierarchical Cumulative Voting is the technique you will use.

 

Step 1

Define the exact set of items that will be prioritized and gather them together in a form that allows them to be easily reviewed. For HCV this often means creating at least two artifacts:

1. A Feature Tree or similar diagram that visually breaks-down the items being prioritized into the appropriate levels of abstraction and groups. [This is not necessary, but the visual structure is very useful to stakeholders and those who will review the prioritization results.]
2. Depending on the level of information you have on the items being prioritized, you may also want to create an associated document (index cards, Word document, sheets of paper, etc.) that has the detailed information for each item clustered in the same way that it is represented in the diagram. This way participants can easily reference more information (assuming it is available) about the items they are prioritizing.

The diagram below is a highly simplified example of the visual component.

 

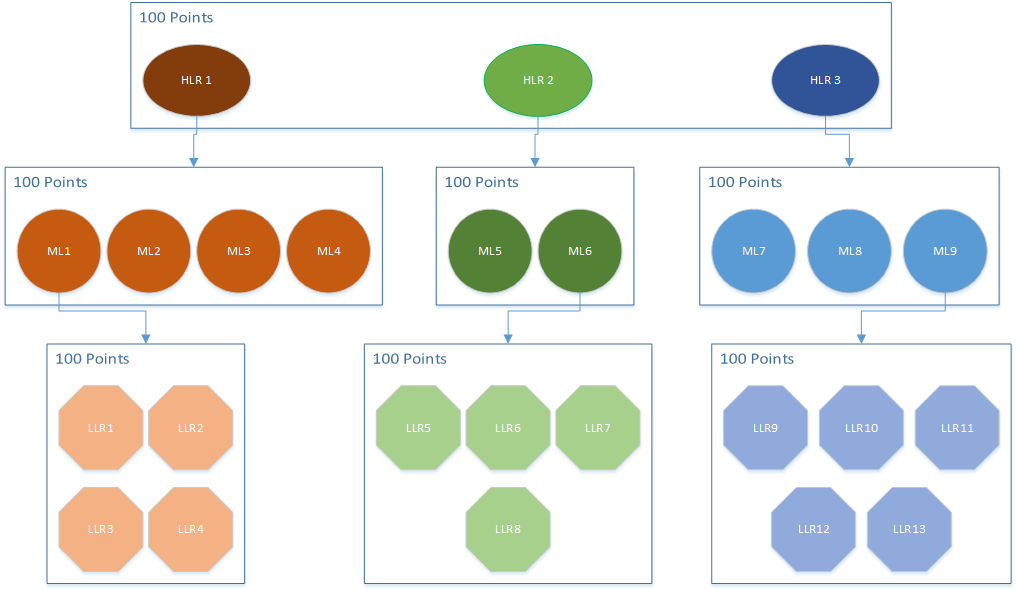
The diagram above provides a simple overview of the process.  After the items are defined at their highest level of abstraction, 100 points are allocated among HLR1-3 by the voters.  At the mid-level of abstraction, another 100 points are allocated to the orange set ML1-4, which are the mid-level decomposition of HLR1.  And the process is repeated again for each of the levels of abstraction that further decompose each item.  NOTE that the lower levels are representative of the decomposition of just one each of the mid-level items and that you would repeat the process with the next decomposition abstraction of level of all of the mid-level items.

 

Step 2

Decide how and where each stakeholders vote will be recorded?  The process selected should allow for each stakeholders vote to be recorded separately and without visibility into the votes other stakeholders may make.

 

Step 3

Given the number of items being prioritized, decide upon an appropriate number of units to provide each stakeholder to assign.  It's also a good idea to assign the units a form that has meaning to the stakeholders, such a dollars, man-hours of work, points, or similar forms.

The amount provided to the stakeholder should be of a sufficient level to allow them to assign a small to moderate amount to most of the items while heavily favoring a few select items.  But you also don't want to provide so much that scale becomes meaningless.

For example, if evaluating 25 items, you might provide "$500 dollars" of units for stakeholder assignment.  This allows for a breakdown such as 5 high-priority items assigned $50 each (for $250 total), 5 medium-priority items at around $30 each ($150 total), and 10 low-priority items at $10 each (the last $100 remaining), 5 items getting no value assigned at all.

 

Step 4

Each stakeholder who will be voting should be taken aside (or otherwise engaged away from other prioritizing stakeholders) and asked to assign all of the units they have been provided to the items being prioritized in such a way as to reflect the way they value each item to relation to all of the others.

Each stakeholder should only be allowed to prioritize each set of items ONCE!  And they should do so without knowledge of how others have prioritized the items.  Allowing stakeholders to vote more than once on the same items or to know how other stakeholders have voted opens up the opportunity to try and game the process by adjusting their votes based on the actions of other stakeholders rather than reflecting their own priority.

When using HCV, the process should allow stakeholders to go back and re-vote on any other grouping or level of abstraction as they work through the entire set.  This is because the process of voting on the lower-level (more detailed) items, may cause them to re-evaluate their prior voting allotments.^[1]  However, their prioritization work should still be completed without knowledge of how others have prioritized and once they are done they should not be allowed to go back and change their priorities.

 

Step 5

Up until this point, HCV runs basically the same as many small CV sessions.  However, where HCV becomes complex is when you want to be able to compare the priority of an item in one group with an item in a different group.  In order to make those comparisons, you first have to normalize the votes across the various levels of abstraction.  Say we wanted to compare the priority value of ML1 in the diagram above to the priority values of ML7 and ML8 above, if the votes in the table below were cast by a single stakeholder.

HLR1	50	ML1	35	ML7	70
HLR2	30	ML2	25	ML8	20
HLR3	20	ML3	15	ML9	10
		ML4	25

 

First, we need to determine how many votes have been cast so that we can normalize our values.  There are 3 different groups of 100 votes above (ML 1-4, ML 5-6, and ML 7-9) at the mid-level of abstraction, which results in a normalization factor of 300 (3 groups x 100 votes per group).  To actually normalize the values, you take the number of votes for each specific item you are comparing (for example, if ML1 has 25 votes) and divide that by the normalization factor (300 in this case).  And in order to carry through the proportional weighting of the parent items, you multiply the result by the number of votes each parent received.

When this is followed, we get the calculations below which provide the normalized scores for ML1, ML7 and ML8:

ML1 = (25/300=0.0833 )*50= 4.166

ML7= (70/300=0.233 )*20= 4.660

ML8= (20/300=0.0666 )*20= 1.330

 

Step 6

As you can see, at this point ML7 has a higher overall weighted priority than ML1, despite being decomposed from a lower-priority item.  This is where the compensation factor comes in.  The compensation factor is applied because the number of items in any given sub-group will skew the results in such a way that any item from a sub-group with fewer items can have a higher priority, just because more points may be assigned it because of the smaller number of items being voted on.  So a compensation factor, which is the number of items in a sub-group is applied to adjust for this.

So given that there are 4 items in the sub-group that ML1 is part of, and 3 items in the sub-group that ML7 and ML8 are part of, we apply the compensation factor by taking the scores above and multiplying them by the compensation factor:

ML1 -> 4.166 * 4 = 16.664

ML7 -> 4.660 * 3 = 13.98

ML8 -> 1.330 * 3 = 3.99

As you see the comparison result is now more useful.

 

Step 7

Once all the stakeholders have voted, and normalization has been done, you may still want to apply a weighing factor to the individual normalized voting results that allows you to factor in the relative importance of various stakeholders.  For example, you might apply a weighting of 200% to the normalized votes of your primary sponsor / stakeholder, leave the normalized votes of main secondary stakeholders unchanged (a weighting of 100%), and apply a 65% weighting (multiply each normalized score by 60%) to the 3 tertiary stakeholders votes.

 

Step 8

The last step is to sum up the votes each item got from all stakeholders and map the scores to your diagram and written item information.

 

---

What Should the Results be?

The items with the highest adjusted and normalized score are your highest-priority items and you can make valid comparisons to assess the relative priorities of any items at the same level of abstraction. This gives you a ratio-scale result at every level of abstraction.

 

---

Advantages

• HCV gives a ratio-scale result and can be relatively easily applied to large requirements sets as long as you do the prep-work to break those requirements down into coherent groups.
• Because HCV breaks the voting down into multiple sub-groups, it is somewhat more difficult for smart stakeholders to game the voting process.

 

---

Disadvantages

• Just as with Cumulative Voting, it is inadvisable to repeat voting on the same set of items with the same set of stakeholders once results are known because it introduces a much greater risk of stakeholders gaming the process.^[2]

 

---

Tips

• Make sure you provide enough initial units so that stakeholders can provide meaningful votes.  If there are 25 items being processed and each stakeholder only gets 100 units, the stakeholders may feel that they cannot really indicate their preferences properly.
• As with Cumulative Voting, Excel provides a relatively easy method to present the detailed item information (the requirements) and to record the votes of a single stakeholder.  You can create a single spreadsheet that has the items already clustered into the appropriate groups that you can provide to each stakeholder, and when you get their results it's easy to combine them all into a single spreadsheet for tracking and results analysis.  Put each item for consideration in the first column, with a second column where "votes" can be assigned. Put the total number of units they have above each grouping. Then use a simple Excel function to sum up the votes cast, subtract them from the total assigned, and show how many are left. If you assigned $1000 to vote with on cells B2 through B15, the function would look like:     =1000-SUM(B2:B15)&" dollars remaining!" You can then copy the values to a single spreadsheet and use Excel to calculate the normalizations, weightings, and total values.
• As with Hierarchical MoSCoW, it is worth noting that the structure used above is very similar to a feature tree. So including a feature tree among your elicitation work can give you a big jump on using either Hierarchical MoSCoW or Hierarchical Cumulative Voting as a prioritization technique.

 

---

References

1. Research Paper: Equality in cumulative voting - A systematic review with an improvement proposal. By K. Rinkevics and R. Torkar. 2013.  From the Authors personal copy.
2. Masters Thesis: An Analysis of Cumulative Voting Results. By Kaspars Rinkevics. Blekinge Institute of Technology. 2011.
3. Research Paper: A Comparison of Nine Basic Techniques for Requirements Prioritization. By Mikko Vestola. Helsinki University of Technology.

 

---

Related Resources

• Master's Thesis: A Controlled Experiment on Analytical Hierarchy Process and Cumulative Voting - Investigating Time, Scalability, Accuracy, Ease of use and Ease of learning. By Deepak Sahni. 2007.
• Article: Requirements Prioritization Introduction. By Nancy Mead. 2006. Carnegie Mellon University, reproduced on the Build Security In web site of the U.S. Department of Homeland Security.